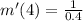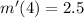Question

(C) Let m be the function defined by m(g(x)) = x. In other words, m and g are inverses. Find m'(4).​

Answer 1

`m'(4)=2.5`

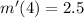
Step-by-step explanation:

The given function m, is defined by
`m(g(x))=x`.

This means m and g are inverse functions.

We want to find m'(4).

We differentiate
`m(g(x))=x` using the chain rule to get:

`m'(g(x))\cdot g'(x)=1`

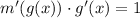
When x=2, we obtain:

`m'(g(2))\cdot g'(2)=1`

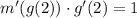
From the table,
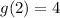`g(2)=4` and
`g'(2)=0.4`

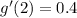
We substitute to get:

`m'(4)\cdot 0.4=1`

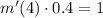
Divide by 0.4

`m'(4)=(1)/(0.4)`

`m'(4)=2.5`