Question

Nick wants to build a rectangular enclosure for his animals. one side of the pen will be against the barn, so he needs no fence on that side. the other three sides will be enclosed with wire fencing. if nick has 700 feet of fencing, you can find the dimensions that maximize the area of the enclosure.

Answer 1

350 ft long facing the barn and 175 ft wide

Explanation:

Let a and b be the length and width of his rectangular fence. Since he has 700 feet of fencing and one side does not need fencing. We have the following constraint equation:

a + 2b = 700

a = 700 - 2b

We want to maximize the following area formula

A = ab

We can substitute a = 700 - 2b

`A = (700 - 2b)b = 700b - 2b^2`

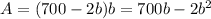
To find the maximum value of this, simply take the 1st derivative, and set it to 0

A' = 700 - 4b = 0

b = 700 / 4 = 175 ft

a = 700 - 2b = 700 - 350 = 350 ft