Answer:
(D) 3
Step-by-step explanation:
The angular momentum is given by:
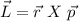
Thus, the magnitude of the angular momenta of both solar systems are given by:
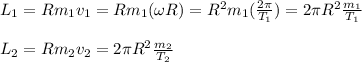
where we have taken that both systems has the same radius.
By taking into account that T1=3T2, we have
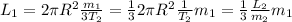
but L1=L2=L:
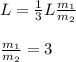
Hence, the answer is (D) 3
HOPE THIS HELPS!!