Question

If right triangle RST, ST = 5, RT = 12, and RS = 13. Find tan (S).

Answer 1

tan(S) =
`(12)/(5)`

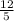
Explanation:

Hi there!

We are given ΔRST, where ST=5, RT=12, and RS=13

We want to find the tangent of angle S (the notation tan(S) means "tangent of angle S")

In trigonometry, tangent refers to the ratio of the opposite side/adjacent side.

The opposite side is the side that is opposite to the angle that we are referencing (in this case, angle S); in this case, that side is RT, which is 12

The adjacent side is the leg that is adjacent to the opposite side; in this case, that side is ST, which we were given as 5

Therefore, tan(S) will be
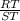`(RT)/(ST)`, or
`(12)/(5)`.

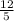Hope this helps!

Answer 2

tan(S) = 12/5

Explanation:

The mnemonic SOH CAH TOA reminds you the tangent ratio is ...

Tan = Opposite/Adjacent

In the given triangle, the side opposite angle S is RT, which has length 12. The side adjacent to angle S is ST, which has length 5. Then the tangent of angle S is ...

tan(S) = RT/ST

tan(S) = 12/5

_____

Additional comment

The rest of the trig functions in this triangle are ...

sin(S) = 12/13

cos(S) = 5/13

tan(R) = 5/12

sin(R) = 5/13

cos(R) = 12/13