Question

Lucia and Marcus are playing a board game. They roll 2 dice (number cubes) to see who goes first. The person who rolls the highest sum gets to go first. If there is a tie, they each roll the dice again. Lucia went first and she rolled a 4 and a 1. Find the probability that Marcus will not get to go immediately after he rolls the dice. Show all of your work below. Express your answer as a fraction in simplest form, a decimal and a percent

Answer 1

5/18, 0.278, 27.8%

Explanation:

In this problem, we basically want to find the probability that Marcus will have a total sum of the 2 dices less than Lucia.

In her throw, Lucia gets a 4 and a 1, so she gets a total sum of 5.

Therefore, we want to find the probability that Marcus will get 5 or less.

The possible combinations that can be obtained when throwing 2 dices are 36 (6 x 6).

Of all these 36 combinations, those that gives a sum of 5 or less are:

1 +1 = 2

1 + 2 = 3

2 + 1 = 3

1 +3 = 4

3 + 1 = 4

1 + 4 = 5

4 + 1 = 5

2 + 2 = 4

2 + 3 = 5

3 + 2 = 5

So, a total of 10 combinations.

Since the probability of an event is:

`p(A)=(s)/(n)`

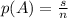
where

s is the number of successfull outcomes

n is the number of total possible outcomes

Here we have

s = 10

n = 36

Therefore the probability here is

`p=(10)/(36)=(5)/(18)=0.278 = 27.8\%`