Question

James has an ice cube tray that makes ice in the shape of spheres rather than cubes. Each sphere of ice has a radius of 22 2 2 cm. One tray makes 66 6 6 spheres.

Answer 1

James has an ice cube tray that makes ice in the shape of spheres rather than cubes. Each sphere of ice has a radius of 2 cm. One tray makes 6 spheres.What is the total volume of ice the tray can make at one time?

Total volume of the tray James have = 201.06 cm^3

Explanation:

Given:

Radius of the spherical ice cube = 2 cm

No. of spheres in the ice cube = 6

We have to find the total volume of the ice tray that can make at one time.

Let the total volume be "V".

Formula to be used:

Volume of sphere =
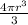`(4\pi r^3 )/(3)` cubic unit.

Total volume =
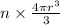`n* (4\pi r^3 )/(3)` cubic unit.

So,

Total volume of the ice tray (V) :

⇒
`V=n* (4\pi r^3 )/(3)`

⇒ Plugging n = 6 and r = 2

⇒
`V=6* (4\pi (2)^3 )/(3)`

⇒
`V=6* (4\pi (8) )/(3)`

⇒
`V=6* (32\pi )/(3)`

⇒
`V=(32* 6\pi )/(3)`

⇒
`V=32* 2\pi`

⇒
`V=201.06\ cm^3`

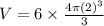
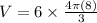
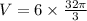
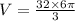
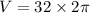
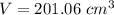
So,

The total volume of ice the tray can make at one time = 201.06 cm^3