Answer: The answer is 79.0°
Explanation:
A quadrilateral will always have 360° and four sides. Keep that in mind, that's a universal rule of geometry.
Here, the sum of all sides is equal to 360°. Therefore, we make an equation:
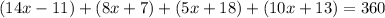
Simplify by adding and subtracting like terms.
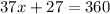
Isolate x by first passing the 27 to the other side.
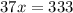
Divide by 37 to isolate x.
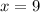
To find m∠B, we plug in x to

which gives you:
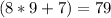
The answer is 79.0°
Curious if it is correct? Let's double check.
Plug in the x=9 to all the x values and add them up. You should get 360, which makes the answer correct.