Question

Mr.Gonzales is replacing a cylindrical air-conditioning duct. He estimates the radius of the duct by folding a ruler to form two 6-in. tangents to the duct. The tangents form an angle. Mr. Gonzales measures the angle bisector from the vertex to the duct. It is about 2.75 inches long. What is the radius of the duct.

Answer 1

The radius of the duct is
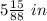`5(15)/(88)\ in` or
`5.17\ in`

Explanation:

we know that

At the point of tangency, the tangent to a circle and the radius are perpendicular lines

so

In the right triangle formed

Applying the Pythagorean Theorem

`(r+2.75)^2=r^2+6^2`

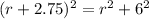
Remember that

`2.75\ in=2(3)/(4)=(11)/(4)\ in`

substitute

`(r+(11)/(4))^2=r^2+6^2`

solve for r

`r^2+(11)/(2)r+(121)/(16)=r^2+36\\(11)/(2)r=36-(121)/(16)`

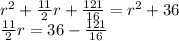
Multiply by 16 both sides

`88r=576-121\\88r=455\\r=(455)/(88)\ in`

convert to mixed number

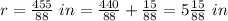`r=(455)/(88)\ in=(440)/(88)+(15)/(88)=5(15)/(88)\ in` ----> exact value

The approximate value is
`5.17\ in`