Question

Find the exact value of sin(θ) for an angle θ with sec(θ) = 5/2 and with its terminal side in Quadrant IV.

​

Answer 1

B

Explanation:

(Sorry about the crude drawing)

The drawing shows what the triangle with a terminal side in Quadrant IV looks like.

Secant is the ratio of the hypotenuse to the adjacent side of the angle. In the given ratio, we can set 5 as the hypotenuse and 2 as the adjacent side (you can see them labeled in the picture).

Now, we want to find sin, which is (opposite)/(hypotenuse). However, we don't know the opposite. We can find it by using the Pythagorean Theorem:

`√(5^2-2^2) =√(25-4) =√(21)`

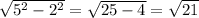
So, the opposite side is
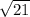`√(21)`. But, we see that since it's in the fourth quadrant, it must be negative, so we have opposite =
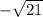`-√(21)`. Now, we can find the ratio because hypotenuse = 5:

sin(θ) =
`-√(21) /5`.

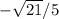Thus, the answer is B.

Hope this helps!

Answer 2

Option B

Explanation:

Please see attached picture for full solution.

Y has to be negative since it lies below the x axis.

In 4th quadrant, only the cosine of an angle is positive.