Question

Figure ABCD is a parallelogram.

What are the lengths of line segments AB and BC?
3
-2
в
• AB = 4, BC = 16
AB = 4; BC = 8
AB = 10; BC = 20
• AB = 10; BC = 28
y
+
6

Answer 1

Given:

Given that ABCD is a parallelogram.

The length of AB is 3y - 2.

The length of BC is x + 12.

The length of CD is y + 6.

The length of AD is 2x - 4.

We need to determine the length of AB and BC.

Value of y:

We know the property that opposite sides of a parallelogram are congruent, then, we have;

`AB=CD`

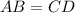
Substituting the values, we get;

`3y-2=y+6`

`2y-2=6`

`2y=8`

`y=4`

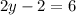
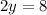
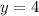
Thus, the value of y is 4.

Value of x:

We know the property that opposite sides of a parallelogram are congruent, then, we have;

`AD=BC`

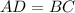
Substituting the values, we get;

`2x-4=x+12`

`x-4=12`

`x=16`

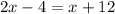
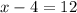
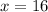
Thus, the value of x is 16.

Length of AB:

The length of AB can be determined by substituting the value of y in the expression 3y - 2.

Thus, we have;

`AB=3(4)-2`

`=12-2`

`AB=10`

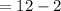
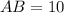
Thus, the length of AB is 10 units.

Length of BC:

The length of BC can be determined by substituting the value of x in the expression x + 12.

Thus, we have;

`BC=16+12`

`BC=28`

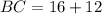
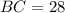
Thus, the length of BC is 28 units.

Hence, the length of AB and BC are 10 units and 28 units respectively.