Question

The number of times per minute that a hummingbird's wings flap is normally distributed with a mean of 145 and a standard deviation of 2. Part A: What is the probability that a randomly selected hummingbird flaps its wings more than 151 times a minute? Part B: What percentage of hummingbirds flap their wings between 141 and 149 times per minute? Part C: A hummingbird that flaps its wings 147 times a minute is in the _______________ percentile.

Answer 1

a) 0.0013

b) 0.9544

c) 84.13 percentile.

Explanation:

We are given the following information in the question:

Mean, μ = 145

Standard Deviation, σ = 2

We are given that the distribution of wings flap is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

a) P( flaps its wings more than 151 times a minute)

`P( x > 151) = P( z > \displaystyle(151 - 145)/(2)) = P(z > 3)`

`= 1 - P(z \leq 3)`

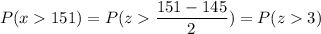
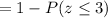
Calculation the value from standard normal z table, we have,

`P(x > 151) = 1 - 0.9987 = 0.0013`

b) P( flap their wings between 141 and 149 times per minute)

`P(141 \leq x \leq 149)\\\\ = P(\displaystyle(141 - 145)/(2) \leq z \leq \displaystyle(149-145)/(2))\\\\ = P(-2 \leq z \leq 2)\\\\= P(z \leq 2) - P(z < -2)\\= 0.9772 - 0.0228 = 0.9544`

c) Percentile of hummingbird that flaps its wings 147 times a minute

`P( x < 147) = P( z < \displaystyle(147 - 145)/(2)) = P(z < 1)`

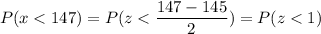
Calculation the value from standard normal z table, we have,

`P(x < 147) = 0.8413`

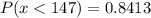
Thus, A hummingbird that flaps its wings 147 times a minute is in the 84.13 percentile.