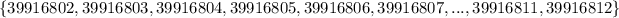Question

Let n be any natural number greater than 1. Explain why the numbers n! 2, n! 3, n! 4, ..., n! n must all be composite. (This exercise shows that it is possible to find arbitrarily long sequences of consecutive composite numbers.)

Answer 1

Because each term of the sequence generates numbers with more than 1 and itself as dividers

Explanation:

Just for the sake of correction.

`1. Explain\: why\: the\: numbers\: n! +2, n!+ 3, n!+ 4, ..., n! \\n \:must\: all\: be\: composite.`

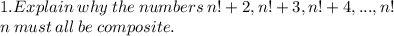
1) Let's consider that

n! =n(n-1)(n-2)(n-3)...

2)And examine some numbers of that sequence above:

`n!+2`

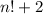
Every Natural number plugged in n, and added by two will a be an even number not only divisible by two, but in some cases by other numbers for example,n=4, then 4!+2=26 which has four dividers.

3) Similarly, the same happens to

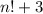`n!+3` and
`n!+4`

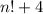
Where we can find many dividers.

There's an example of a sequence, let's start with a prime number greater than 1

Let n=11

`\left \{ n!+2,n!+3,n!+4,n!+5,n!+6,...n!+n. \right \}\\\left \{ 11!+2,11!+3,11!+4,11!+5,11!+6,11!+7,11!+8,...11!+11 \right \}\\\\`

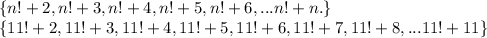
That's a long sequence of consecutive composite numbers, n=11.

`\left \{39916802, 39916803,39916804,39916805,39916806,39916807,...,39916811,39916812 \right \}`