Answer:
Work done by the gas for the given volume and pressure
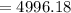 pounds foot
pounds foot
Step-by-step explanation:
Given
Pressure applied
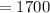 pounds per square foot
pounds per square foot
Initial Volume
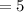 cubic feet
cubic feet
Final Volume
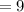 cubic feet
cubic feet
As we know pressure is inversely proportional to V
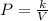
where k is the proportionality constant
V is the volume and
P is the pressure
Work done
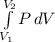
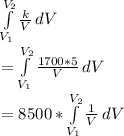
Integrating the above equation, we get-
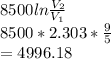
Work done by the gas for the given volume and pressure
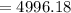 pounds foot
pounds foot