Question

Determine the margin of error, m m , of a 90% confidence interval for the mean IQ score of all students with the disorder. Assume that the standard deviation IQ score among the population of all students with the disorder is the same as the standard deviation of IQ score for the general population, σ = 15 σ=15 points. Give your answer precise to at least two decimal places

Answer 1

The margin of error is 6.45.

Explanation:

The complete question is:

As an early intervention effort, a school psychologist wants to estimate the average score on the Stanford-Binet Intelligence Scale for all students with a specific type of learning disorder using a simple random sample of 36 students with the disorder.

Determine the margin of error, of a 99% confidence interval for the mean IQ score of all students with the disorder. Assume that the standard deviation IQ score among the population of all students with the disorder is the same as the standard deviation of IQ score for the general population, σ = 15 points.

The (1 - α)% confidence interval for population mean μ is:

`CI=\bar x\pm z_(\alpha/2)*(\sigma)/(√(n))`

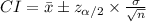
The margin of error for this interval is:

`MOE= z_(\alpha/2)*(\sigma)/(√(n))`

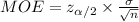
Given:

n = 36

σ = 15

(1 - α)% = 99%

Compute the critical value of z for 99% confidence level as follows:

`z_(\alpha/2)=z_(0.01/2)=z_(0.005)=2.58`

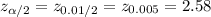
*Use a z-table.

Compute the value of MOE as follows:

`MOE= z_(\alpha/2)*(\sigma)/(√(n))`

`=2.58*(15)/(√(36))`

`=2.58* 2.5\\=6.45`

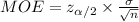
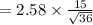
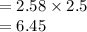
Thus, the margin of error is 6.45.