Question

Use the graph of f to calculate
`\int\limits^4_0 {f(t)} \, dt`. PLEASE HELP!

Answer 1

You should already be aware that the definite integral of
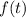`f(t)` is equivalent to the signed area under the curve of

`\displaystyle\int_0^1f(t)\,\mathrm dt`

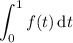
corresponds the area of the triangle on the left, and

`\displaystyle\int_1^4f(t)\,\mathrm dt`

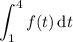
is the area of the trapezoid in the middle. You should know how to compute the area of these shapes.

We end up with

`\displaystyle\int_0^4f(t)\,\mathrm dt=-\frac{1*2}2+\frac{(1+3)*2}2=3`

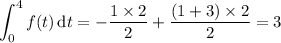
since the triangle has height 2 and base 1, and the trapezoid has height 2 with two base lengths 1 and 3.

Edit: The area under the curve is highlighted red in the attachment below. It's the area between the curve and the horizontal axis, but it's also signed, meaning the area below the axis is negative, and the area above the axis is positive.