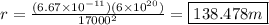Question

If a satelite with a mass of 9 x 10^2 kg is placed in an orbit around a planet with a mass of 6 x 10^20 kg, at a speed of 17000 m/s, find the distance from the center of the planet to the satelite.

Answer 1

Hi there!

We can begin by deriving an equation for the orbital radius.

For an object orbiting the earth, it is experiencing a centripetal force due to the force of gravitation.

Recall Newton's Law of Universal Gravitation:

`F_g = (Gm_1m_2)/(r^2)`

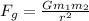
G = Gravitational Constant (6.67 × 10⁻¹¹ Nm²/kg²)

m = masses (kg)
r = radius (m)

This is equivalent to the satellite's centripetal force experienced:

`F_c = (m_sv^2)/(r)`

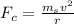
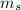`m_s` = mass of satellite (kg)

v = velocity (m/s)

r = radius (m)

Set the two equal, and rearrange for the orbital radius of the satellite.

`(Gm_sm_p)/(r^2) = (m_sv^2)/(r)\\\\(Gm_p)/(r) = v^2\\\\r = (Gm_p)/(v^2)`

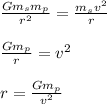
Notice that the orbital radius of the satellite does NOT depend on the satellite's mass. (we canceled it out).

Now, plug in the given values.

`r = ((6.67* 10^(-11))(6* 10^(20)))/(17000^2) = \boxed{138.478 m}`