Answer:
B, C, E
Explanation:

If we were to consider expanding the expression ( x + y )^2, take a look at the procedure below;
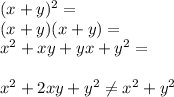
Thus, the first option is incorrect
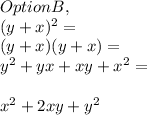
x^2 + 2xy + y^2 is similar to the result of the expansion of ( x + y )^2, so the second option is correct

Grouping like terms, x( x + y ) + y( x + y ) = ( x + y )^2, and thus the third option is correct
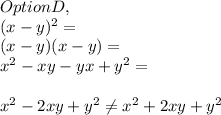
As noted before, x^2 - 2xy + y^2 is not x^2 + 2xy + y^2, so the fourth option is incorrect
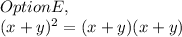
And thus, Option E is correct!