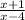Question

12. Find the perimeter of the triangle below:
please help show steps thank you :)
​

Answer 1

Given:

The lengths of the three sides of the triangle are
`(3)/(x-4)`,
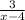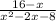`(16-x)/(x^(2)-2 x-8)` and
`(x+5)/(x+2)`

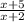
We need to determine the perimeter of the triangle.

Perimeter of the triangle:

The perimeter of the triangle can be determined by adding all the three sides.

Thus, we have;

`Perimeter=(3)/(x-4)+(16-x)/(x^(2)-2 x-8)+(x+5)/(x+2)`

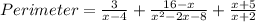
Factoring the term
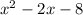`x^2-2x-8`, we get,
`(x-4)(x+2)`

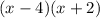
Substituting, we get;

`Perimeter=(3)/(x-4)+(16-x)/((x-4)(x+2))+(x+5)/(x+2)`

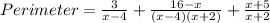
Taking LCM , we have;

`Perimeter=(3(x+2)+16-x+(x+5)(x-4))/((x-4)(x+2))`

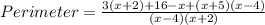
Simplifying the numerator, we get;

`Perimeter=(3x+6+16-x+x^2-4x+5x-20)/((x-4)(x+2))`

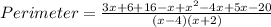
Adding the like terms in the numerator, we get;

`Perimeter=(x^2+3x+2)/((x-4)(x+2))`

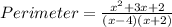
Factoring the numerator, we get;

`Perimeter=((x+2)(x+1))/((x-4)(x+2))`

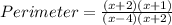
Cancelling the common terms, we have;

`Perimeter=(x+1)/(x-4)`

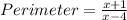
Thus, the perimeter of the triangle is
`(x+1)/(x-4)`