Question

Please help kind of urgent i only have 100 points so please help thanks:)

Answer 1

Let's solve

`\\ \rm\Rrightarrow sin\theta=(√(3))/(2)`

`\\ \rm\Rrightarrow \theta=sin^(-1)\left((√(3))/(2)\right)`

`\\ \rm\Rrightarrow \theta=(\pi)/(3)`

Now

`\\ \rm\Rrightarrow tan\theta=tan(\pi)/(3)`

`\\ \rm\Rrightarrow tan\theta=√(3)`

Answer 2

√3

Explanation:

To recall trigonometric ratios, there is a special acronym known as sohcahtoa which stands for

• sin(x)=opposite/ hypotenuse
• cos(x)=adjacent/hypotenuse
• tan(x)=opposite /hypotenuse

Finding the angle
`\theta`

We are given that,

`\displaystyle \sin( \theta) = ( √(3) )/(2)`

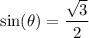
To find the angle
`\theta` , take inverse of sin of both sides,

`\displaystyle { \sin}^( - 1)( \sin( \theta) )= { \sin}^( - 1) \bigg(( √(3) )/(2) \bigg )`

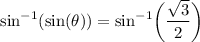
with the help of unit circle,we acquire:

`\displaystyle \boxed{\theta= {60}^( \circ) }`

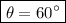
Finding
`\tan\theta`

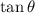
simply plug in the value of theta:

`\tan( {60}^( \circ) )`

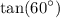
using unit circle,we get:

`\implies \tan( {60}^( \circ) ) = \boxed{√(3) }`

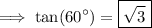
and we're done!