Question

A gardener is fencing off a rectangular area with a fixed perimeter of 72 ft.What is the maximum area?

Answer 1

`324 ft^2`

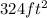
Explanation:

The area of a triangle is given by the product between length and width:

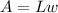`A=Lw` (1)

where

L is the length

w is the width

The perimeter of the rectangle is given by

`p=2L+2w`

In this problem, we know that the perimeter of the rectangle is fixed, and it is

`p=72 ft`

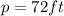
So we have:

`72=2L+2w`

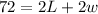
Which can be rewritten as

`w=36-L`

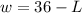
If we substitute this into the formula of the area, (1), we get:

`A=L(36-L)=36L-L^2`

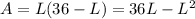
To maximize the area, we have to calculate its derivative and require it to be equal to zero:

`(dA)/(dL)=0`

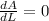
Calculating the derivative,

`(dA)/(dL)=(d)/(dL)(36L-L^2)=36-2L`

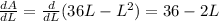
And requiring it to be zero, we find:

`36-2L=0\\L=(36)/(2)=18`

Which means also

`w=36-L=36-18=18`

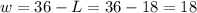
So,

L = 18 feet

w = 18 feet

So the maximum area is achieved when the rectangle has actually the shape of a square.

In such case, the area is:

`A=18\cdot 18=324 ft^2`

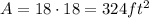
So, this is the maximum area.