Question

Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.63 and standard deviation 0.80.

(a) If a random sample of 25 specimens is selected, what is the probability that the sample average sediment density is at most 3.00?

Answer 1

The probability that the sample average sediment density is at most 3.00 is 0.2090.

Explanation:

Let X = he sediment density (g/cm) of a specimen from a certain region.

The random variable X is normally distributed with mean, μ = 2.63 and standard deviation, σ = 0.80.

A random sample of n = 25 specimens is selected.

The distribution of the sample mean of a normally distributed random variable is also normal.

To compute the probability of the sample mean we need to first compute the z score of the sample mean value. The formula of z-score is:

`z=(\bar X-\mu)/(\sigma/√(n))`

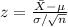
Compute the probability that the sample average sediment density is at most 3.00 as follows:

Apply continuity correction:

`P(\bar X\leq 3.00)=P(\bar X< 3.00-0.50)`

`=P(\bar X<2.50)\\=P((\bar X-\mu)/(\sigma/√(n))<(2.50-2.63)/(0.80/√(25)))`

`=P(Z<-0.81)\\=1-P(Z<0.81)\\=1-0.79103\\=0.20897\\\approx0.2090`

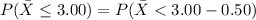
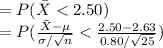
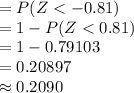
*Use a z-table for the probability.

Thus, the probability that the sample average sediment density is at most 3.00 is 0.2090.