Question

A lake near the arctic circle is covered by a 2 meter thick sheet of ice during the cold winter months. When spring arrives , the warm air gradually melts the ice , causing its thickness to decrease at a constant rate . After 3 weeks , the sheet is only 1.25 meters thick

Answer 1

A lake near the Arctic Circle is covered by a 2-meter-thick sheet of ice during the cold winter months. When spring arrives, the warm air gradually melts the ice, causing its thickness to decrease at a constant rate. After 3 weeks, the sheet is only 1.25 meters thick. Let S(t) denote the ice sheet's thickness S (measured in meters) as a function of time t (measured in weeks). Write the function's formula.

The function's formula is, S(t) = -0.25(t) + 2

Explanation:

Given:

That there is gradual decrease in the thickness of the ice of Arctic circle.

S(t) denote the ice sheet's thickness S ( measured in meters) as a function of time (measured in weeks).

Initial thickness of the sheet of ice, S(t) = 2 m

Numbers of weeks required to melt = 3

After melting its final thickness is = 1.25 m

Considering the decrease at a constant rate we can say that it follows linear pattern or linear equation.

So,

The equation will be of the form y = m(x) + b

Re-arranging the terms:

We have:

S(t) = mt + b

Now we have to find the slope (m) and y-intercept value (b).

Plugging
`t=0,\ S(t)=2` as the initial thickness is of
`2` meters.

⇒
`S(t) = mt + b`

⇒
`2=(m* 0) + b`

⇒
`2=0+b`

⇒
`2=b`

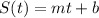
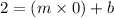
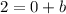
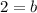
Plugging
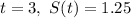`t = 3,\ S(t) = 1.25` as after
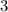`3` weeks it melts gradually.

⇒
`S(t) = mt + b`

⇒
`1.25=3m + b`

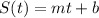
⇒Putting b=2 from above equation.

⇒
`1.25=3m + 2`

⇒
`1.25-2=3m + 2-2`

⇒
`-0.75=3m`

⇒
`(-0.75)/(3) =(3m)/(3)`

⇒
`-0.25=m`

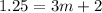
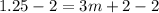
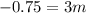
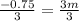
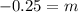
Plugging the above values in S(t) =mt+b.

⇒ S(t) =mt+b

⇒
`S(t)=-0.25(t)+2`

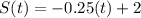
Hence

The function's formula is, S(t) = -0.25(t) + 2 i.e. S(t) = 2 - 0.25(t)