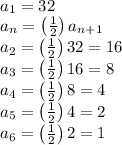Question

Enter both an explicit and recursive rule for the geometric sequence that models the situation. use the sequence to answer the question asked about the situation. the alphaville youth basketball committee is planning a single-elimination tournament (for all the games at each round, the winning team advances and the losing team is eliminated). the committee wants the winning team to play 6 games. how many teams should the committee invite?

Answer 1

`32` teams

Explanation:

Let's do it by parts.

Let's consider a fact: there has to be only one winner. After six games:

So,
`a_(6)=1`

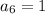
Since it's a decreasing Geometric Sequence (we have to lead to one winner), and each match two teams play, the beaten one leaves the championship.

`r=((1)/(2))`

`a_(1)=?`

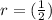
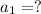
a) Explicit Rule (Formula):

`a_(6)=1,a_(1)=?r=(1)/(2)\\1=a_(1)\left ( (1)/(2) \right )^(6-1)\\1=a_(1)\left ( (1)/(2) \right )^(5)\\1=(a_(1))/(32)\\a_(1)=32`

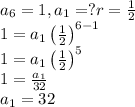
That's to say the tournament started with 32 teams

`\{32,16,8,4,2,1\}`

b) Recursive Rule

If we have the first term of the Geometric Sequence we can recursively find the subsequent terms. The Recursive Rule is useful when we have the prior term and we need the following one. Also, to derive the explicit rule.

`a_(1)=32\\a_(n)=\left ( (1)/(2) \right )a_(n+1)\\a_(2)=\left ( (1)/(2) \right )32=16\\a_(3)=\left ( (1)/(2) \right )16=8\\a_(4)=\left ( (1)/(2) \right )8=4\\a_(5)=\left ( (1)/(2) \right )4=2\\a_(6)=\left ( (1)/(2) \right )2=1\\`

`\{32,16,8,4,2,1\}`