Question

A rectangular garden measuring 13 meters by 15 meters is to have a gravel pathway of constant width built all around it. There is enough gravel to cover 80 square meters. Enter an inequality that represents all possible widths(w), in meters, of the pathway.

Answer 1

Let w represent width of the pathway.

We have been given that a rectangular garden measuring 13 meters by 15 meters is to have a gravel pathway of constant width built all around it.

Since pathway will be on all sides, so new length and width of garden with pathway would be
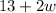`13+2w` by
`15+2w`.

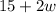We are also told that there is enough gravel to cover 80 square meters. This means that area f pathway should be equal to 80 square meters.

The area of the pathway will be equal to area of garden with new dimensions minus area of garden with original dimensions.

We know that area of rectangle is width times length.

`\text{Area of pathway}=(15+2w)(13+2w)-15(13)`

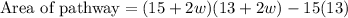
Since we are asked to write an inequality that represents all possible widths(w), in meters, of the pathway, so area of pathway should be less than or equal to 80 square meters.

`(15+2w)(13+2w)-15(13)\leq 80`

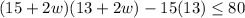
Therefore, our required inequality would be
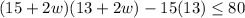`(15+2w)(13+2w)-15(13)\leq 80`.