Question

Suppose a baby food company has determined that its total revenue R for its food is given by R = − x 3 + 39 x 2 + 945 x where R is measured in dollars and x is the number of units (in thousands) produced. What production level will yield a maximum revenue?

Answer 1

35,000 units

Explanation:

Total revenue is:

`R = -x^3+39x^2+945x`

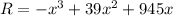
The maximum revenue is attained at the production level for which the derivate of the revenue function is zero:

`R = -x^3+39x^2+945x\\R'=0=-3x^2+78x+945\\x=(-b\pm√(78^2-(4*(-3)*945)) )/(-6)\\x_1=35\\x_2=-9`

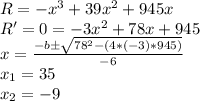
Since production cannot be negative, revenue will be at a maximum when x = 35, or when the production level is 35,000 units.