Question

A recent survey conducted by Wall Street Journal indicates that the average reading time of 100 its readers/participants was 45 minutes and the standard deviation was 20 minutes. The journal is now planning another survey study. If the acceptable error is 3 minutes and a confidence level of 99% is desired, what would be the minimum sample size needed for the upcoming survey?

Answer 1

The minimum sample size needed for the upcoming survey

n = 289

Explanation:

Explanation:-

step:- (i)

Given A recent survey conducted by Wall Street Journal indicates that the average reading time of 100 its readers/participants was 45 minutes and the standard deviation was 20 minutes

sample size n= 100

mean =45 min and standard deviation = 20 minutes

If the acceptable error is 3 minutes and a confidence level of 99% is desired

Given margin of error is '3' min

Step(ii):-

Margin error

We know that margin of error =
`z_(0.99) (S.D)/(√(n ) )`

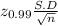
Now we determine the sample size

`n = ((z_(0.99)S.D )/(M.E) )^2`

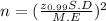
The 99% of level of significance 'Z' value = 2.57

`n = ((2.57 (20) )/(3) )^2`

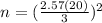
n = (17)^2

n = 289

Conclusion:-

The minimum sample size needed for the upcoming survey

n = 289

Verification:-

Margin error =
`Margin error=z_(0.99) (S.D)/(√(n ) )=(2.57 (20))/(√(289) )= 3.02`

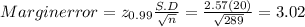
Given data of margin error also =3

so both are equal

There fore the minimum sample size needed for the upcoming survey

n = 289