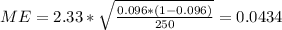Question

A company receives shipments of a component used in the manufacture of a component for a high-end acoustic speaker system. When the components arrive, the company selects a random sample from the shipment and subjects the selected components to a rigorous set of tests to determine if the components in the shipments conform to their specifications. From a recent large shipment, a random sample of 250 of the components was tested, and 24 units failed one or more of the tests. a.At the 98% level of confidence, what is the margin of error in the point estimate of the proportion of components in the shipment that fail to meet the company's specifications

Answer 1

`ME= 2.33*\sqrt{(0.096*(1-0.096))/(250)}= 0.0434`

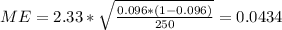
Explanation:

For this case we have a sample size of n = 250 units and in this sample they found that 24 units failed one or more of the tests.

We are interested in the proportion of units that fail to meet the company's specifications, and we can estimate this with:

`\hat p = (24)/(250)= 0.096`

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The confidence interval for a proportion is given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

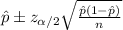
For the 98% confidence interval the value of
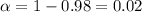`\alpha=1-0.98=0.02` and
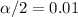`\alpha/2=0.01`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=2.33`

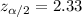
And the margin of error would be:

`ME= 2.33*\sqrt{(0.096*(1-0.096))/(250)}= 0.0434`