Question

Determine the farthest away a car can be at night so that your eyes can resolve the two headlights. Assume that the the diameter of your pupil is 0.50 cm, the dominant wavelength emitted by headlights is 500 nm and car headlights are about 1.3 m apart.

Answer 1

By trigonometric relationship, small angles can be equivalent to the equivalent of the sine of the angle or its trigonometric fraction of the hypotenuse and the opposite leg. Under this relationship we will have at the same time the Rayleigh Criterion by which the angle is also defined as 1.22 times the wavelength and the diameter. For the first mention we have then,

`\theta = (y)/(L)`

By Rayleigh Criterion,

`\theta = (1.22\lambda)/(d)`

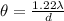
Equating both expression,

`(y)/(L)=(1.22\lambda)/(d)`

`L = (y d)/(1.22\lambda)`

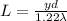
Our values are given as,

`y = 1.3m`

`d = 0.5cm = 0.005m`

`\lambda = 500nm = 500*10^(-9)m`

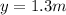
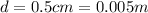
Replacing,

`L = ((1.3m)(0.005m))/(1.22 (500*10^(-9)m))`

L = 10.655km

Therefore the arthest away a car can be at night so that your eyes can resolve the two headlights is 10.655km