Question

A personnel director in a particular state claims that the mean annual income is the same in one of the​ state's counties​ (County A) as it is in another county​ (County B). In County​ A, a random sample of 18 residents has a mean annual income of $ 40 comma 400 and a standard deviation of $ 8700. In County​ B, a random sample of 8 residents has a mean annual income of $ 39 comma 200 and a standard deviation of $ 6000. At alphaequals0.10​, answer parts​ (a) through​ (e). Assume the population variances are not equal. Assume the samples are random and​ independent, and the populations are normally distributed.

Answer 1

a) The hypothesis that the mean annual income is the same could not be rejected. There is no enough evidence to claim they are different.

b) The critical values for this two-sided test are t=±1.711.

Explanation:

The question is incomplete:

(a) Identify the claim and state H0 and Ha.

Which is the correct claim​ below?

(b) Find the critical​ value(s) and identify the rejection​ region(s).

Enter the critical​ value(s) below.

We have an hypothesis test on the difference of two means.

The null and alternative hypothesis are:

`H_0: \mu_a-\mu_b=0\\\\H_a: \mu_a-\mu_b\\eq 0`

The claim of the alternative hypothesis is that the mean annual income is different in County A and County B.

The null hypothesis is that the mean annual income is equal in both counties.

The significance level is α=0.10.

The sample from County A has a mean of S40,400, a s.d. of $8,700 and a sample size of 18 residents.

The sample from County B has a mean of S39,200, a s.d. of $6,000 and a sample size of 8 residents.

The standard error of the difference of means is:

`\sigma_d=\sqrt{(\sigma_a^2)/(n_a)+(\sigma_b^2)/(n_b)}=\sqrt{(8700^2)/(18)+(6000^2)/(8)}=√(8705000)=2950`

The degrees of freedom are:

`df=n_a+n_b-2=18+8-2=24`

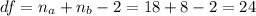
Then, the test statistic is:

`t=(\Delta M-\Delta \mu)/(\sigma_d) =((40,400-39,200)-0)/(2950) =(1200)/(2950)=0.407`

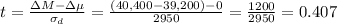
For a statistic t=0.407, and df=24, the P-value is P=0.69. As the P-value is bigger than the significance level, the null hypothesis failed to be rejected.

If we would use the critial value approach, we would have to calculate the critical values for t, for df=24, two sided test and α=0.10.

The critical values, looking in a table, are t=1.711.