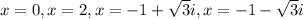Given:
The given function is
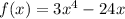
We need to determine the zeros of the function.
Zeros of the function:
The zeros of the function are the values that makes the function's value equal to zero.
The zero of the function can be determined by substituting f(x) = 0 in the function.
Thus, we have;
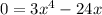
Switch sides, we get;
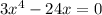
Let us factor out the common term 3x.
Thus, we have;
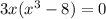
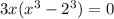
Using the identity,
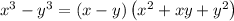 , we get;
, we get;
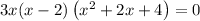
Let us solve using the zero factor principle.
Thus, we have;
If
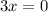 then
then
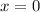
If
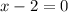 then
then
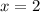
If
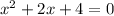 then
then
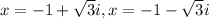 (solving using the quadratic formula)
(solving using the quadratic formula)
Thus, the zeros of the function are