Question

What is the sum of the sequence?

−32+(−34)+(−36)+...+(−778)+(−780)=

Is it -152250 I need a good explanation!!!

Answer 1

The sum of the sequence is -152250.

Explanation:

Given : Sequence
`-32+(-34)+(-36)+...+(-778)+(-780)`

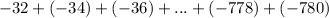
To find : What is the sum of the sequence?

Solution :

The given sequence is in Arithmetic sequence as the difference between them is same.

Where, the first term is a=-32

The common difference is
`d=a_2-a_1`

`d=(-34)-(-32)`

`d=-34+32`

`d=-2`

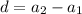
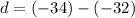
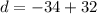
The last term is l=-780.

The last term formula is
`l=a+(n-1)d`

`-780=-32+(n-1)(-2)`

`(-780+32)/(-2)=n-1`

`374=n-1`

`n=375`

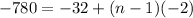
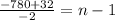
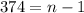
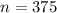
The sum of n terms formula is

`S_n=(n)/(2)[a+l]`

`S_(375)=(375)/(2)[-32+(-780)]`

`S_(375)=(375)/(2)[-812]`

`S_(375)=375* (-406)`

`S_(375)=-152250`

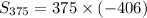
Therefore, the sum of the sequence is -152250.