Question

If VW is 10 cm, find the length of VR⌢. Round to the nearest hundredth (two decimal places).

find the length of VR=

Answer 1

Given:

Given that the length of VW is 10 cm.

The central angle is 127°

We need to determine the arc length of VR.

Arc length of VR:

The arc length of VR can be determined using the formula,

`Arc \ length = (\theta)/(360)* 2 \pi r`

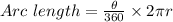
Substituting
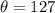`\theta=127` and r = 10, we get;

`Arc \ length = (127)/(360)* 2 (3.14)(10)`

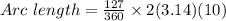
Simplifying the terms, we get;

`Arc \ length = (7975.6)/(360)`

`Arc \ length = 22.154`

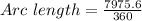
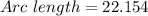
Rounding off to the nearest hundredth, we get;

`Arc \ length = 22.15`

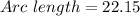
Thus, the arc length of VR is 22.15 cm