Question

Assume that the national credit card interest rate is 12.83 percent. A study of 62 college students finds that their average interest rate is 14 percent with a standard deviation of 9.3 percent. What is the 95 percent confidence interval for this single-sample t test?

a. [6.94, 11.66]
b. [11.64, 16.36]
c. [10.47, 15.19]
d. [12.99, 15.01]

Answer 1

b) 95 percent confidence interval for this single-sample t test

[11.64, 16.36]

Explanation:

Explanation:-

Given data a study of 62 college students finds that their average interest rate is 14 percent with a standard deviation of 9.3 percent.

Sample size 'n' =62

sample mean x⁻ = 14

sample standard deviation 'S' = 9.3

95 percent confidence interval for this single-sample t test

The values are
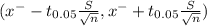`(x^(-) - t_(0.05) (S)/(√(n) ) ,x^(-)+t_(0.05)(S)/(√(n) ))` the 95 percent confidence interval for the population mean 'μ'

Degrees of freedom γ=n-1=62-1=61

t₀.₀₅ = 1.9996 at 61 degrees of freedom

`(14 - 1.9996(9.3)/(√(62) ) ,14+1.9996(9.3)/(√(62) ))`

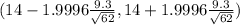
(14-2.361 , 14 + 2.361)

[(11.64 , 16.36]

Conclusion:-

95 percent confidence interval for this single-sample t test

[11.64, 16.36]