Question

An electron that has a velocity with x component 1.6 × 106 m/s and y component 2.4 × 106 m/s moves through a uniform magnetic field with x component 0.025 T and y component -0.16 T.

(a) Find the magnitude of the magnetic force on the electron.
(b) Repeat your calculation for a proton having the same velocity.

Answer 1

(a) 5.056 x 10^-14 N

(b) 5.056 x 10^-14 N

Step-by-step explanation:

X component of velocity of electron is 1.6 × 10^6 m/s

Y component of velocity of electron is 2.4 × 10^6 m/s

X component of magnetic field is 0.025 T

Y component of magnetic field is -0.16 T

charge on electron, q = - 1.6 x 10^-19 C

Write the velocity and magnetic field in the vector forms.

`\overrightarrow{v}=1.6* 10^(6)\widehat{i}+2.4* 10^(6)\widehat{j}`

`\overrightarrow{B}=0.025\widehat{i}-0.16\widehat{j}`

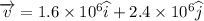
The force on the charge particle when it is moving in the magnetic field is given by

`\overrightarrow{F}=q\left ( \overrightarrow{v}* \overrightarrow{B} \right )`

(a) Force on electron is given by

`\overrightarrow{F}=-1.6* 10^(-19)\left ( 1.6* 10^(6)\widehat{i}+2.4* 10^(6)\widehat{j} \right )* \left ( 0.025\widehat{i}-0.16\widehat{j} \right )`

`\overrightarrow{F}=5.056* 10^(-14)\widehat{k}`

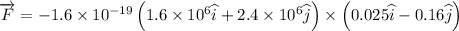
Magnitude of force is 5.056 x 10^-14 N.

(b) Force on a proton is given by

`\overrightarrow{F}=1.6* 10^(-19)\left ( 1.6* 10^(6)\widehat{i}+2.4* 10^(6)\widehat{j} \right )* \left ( 0.025\widehat{i}-0.16\widehat{j} \right )`

`\overrightarrow{F}=-5.056* 10^(-14)\widehat{k}`

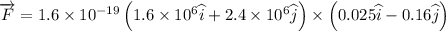
Magnitude of force is 5.056 x 10^-14 N.

Thus, the magnitude of force remains same but the direction of force is opposite to each other.

Step-by-step explanation: