Answer:
(a) Null Hypothesis,
 :
:
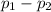
 0 or
0 or



Alternate Hypothesis,
 :
:
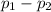 > 0 or
> 0 or
 >
>

(b)
 = sample proportion of men =
= sample proportion of men =
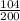 = 0.52
= 0.52
 = sample proportion of women =
= sample proportion of women =
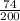 = 0.37
= 0.37
(c) P-value is 0.0011.
Explanation:
We are given that Adecco Workplace Insights Survey sampled men and women workers and asked if they expected to get a raise or promotion this year (USA Today, February 16, 2012).
Suppose the survey sampled 200 men and 200 women. If 104 of the men replied yes and 74 of the women replied yes.
Let
 = population proportion of men who replied yes
= population proportion of men who replied yes
 = population proportion of women who replied yes
= population proportion of women who replied yes
(a) Null Hypothesis,
 :
:
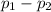
 0 or
0 or


 {means that the population proportion of men is less than or equal to the population proportion of women}
{means that the population proportion of men is less than or equal to the population proportion of women}
Alternate Hypothesis,
 :
:
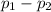 > 0 or
> 0 or
 >
>
 {means that the population proportion of men is more than the population proportion of women}
{means that the population proportion of men is more than the population proportion of women}
(b)
 = sample proportion of men =
= sample proportion of men =
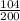 = 0.52
= 0.52
 = sample proportion of women =
= sample proportion of women =
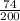 = 0.37
= 0.37
The test statistics that will be used here is Two-sample z proportion statistics;
T.S. =
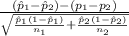 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of men who replied yes = 0.52
= sample proportion of men who replied yes = 0.52
 = sample proportion of women who replied yes = 0.37
= sample proportion of women who replied yes = 0.37
 = sample of men = 200
= sample of men = 200
 = sample of women = 200
= sample of women = 200
So, test statistics =
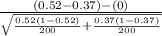
= 3.05
Now at 0.01 significance level, the z table gives critical value of 2.3263 for right-tailed test. Since our test statistics is more than the critical value of z so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.
Therefore, we conclude that the population proportion of men is greater than the population proportion of women.
P-value is given by the following formula;
P(Z > 3.05) = 1 - P(Z
 3.05)
3.05)
= 1 - 0.99886 = 0.0011
Hence, the p-value is 0.0011.