Question

A United Nations report shows the mean family income for Mexican migrants to the United States is $27,150 per year. A FLOC (Farm Labor Organizing Committee) evaluation of 30 Mexican family units reveals a mean to be $29,500 with a sample standard deviation of $11,150. Does this information disagree with the United Nations report? Apply the 0.01 significance level.

(a) State the null hypothesis and the alternate hypothesis.

H0: µ = _____
H1: µ ? ____
(b) State the decision rule for .01 significance level. (Round your answers to 3 decimal places.)

Reject H0 if t is not between______ and ________
(c) Compute the value of the test statistic. (Round your answer to 2 decimal places.)

Value of the test statistic_______
(d) Does this information disagree with the United Nations report? Apply the 0.01 significance level.

Answer 1

(a) H₀: µ = $27,150 vs. Hₐ: µ ≠$27,150.

(b) Reject H₀ if
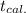`t_(cal.)` is not between -2.756 and 2.756.

(c) The value of the test statistic
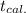`t_(cal.)` is, 1.154.

(d) The information does not disagrees with the United Nations report.

Explanation:

A single mean test is applied to test whether the population mean family income for Mexican migrants to the United States is different from $27,150 per year.

(a)

The hypothesis is:

H₀: The mean family income for Mexican migrants to the United States is $27,150 per year, i.e. µ = $27,150.

Hₐ: The mean family income for Mexican migrants to the United States is $27,150 per year, i.e. µ ≠$27,150.

(b)

The decision rule is:

If the test statistic value,
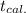`t_(cal.)` lies outside the interval
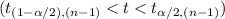`(t_((1-\alpha/2), (n-1))<t<t_(\alpha/2, (n-1)))` then the null hypothesis will be rejected.

Compute the critical values for α = 0.01 and degrees of freedom, (n -1) = 29 as follows:

`t_((1-\alpha/2), (n-1))=-2.756`

`t_(\alpha/2, (n-1))=2.756`

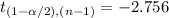
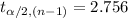
Thus, the rejection region is:

Reject H₀ if
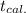`t_(cal.)` is not between -2.756 and 2.756.

(c)

The information provided is:

`\bar x=\$29500\\s=\$11150\\n=30\\\alpha =0.01`

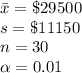
Since the population standard deviation is not given we will use a t-test.

The t-statistic is given by,

`t=(\bar x-\mu)/(s/√(n))=(29500-27150)/(11150/√(30))=1.154`

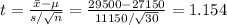
Thus, the value of the test statistic
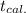`t_(cal.)` is, 1.154.

(d)

The calculated t-statistic is, t = 1.154.

The test statistic value lies in the range (-2.756, 2.756).

Thus, the null hypothesis will not be rejected at 1% level of significance.

Hence, concluding that the information does not disagrees with the United Nations report.