Question

A shipping company must design a closed rectangular shipping crate with a square base. The volume is 1152ft3. The material for the top and sides costs $2 per square foot and the material for the bottom costs $7 per square foot. Find the dimensions of the crate that will minimize the total cost of material.

Answer 1

The cost function has a minimum at x = 14.461 and z = 5.508

Explanation:

We want to find the optimal price. For that we need to first find the price function which would be

`f(x,z) = 2(2x^2) +7(4xz)`

Where
`x` is the measure of the side on the bottom and
`z` is the height of the crate.

And we also know that the volume must be

`V = x^2 z = 1152`

From the volume equation we solve for
`z` and get

`z = (1152)/(x^2)`

So the function we have to optimize is this.

`f(x)= 4x^2 +(24192)/(x)`

After you find the derivative and equal that to zero you find that the cost function has a minimum at

x = 14.461 and z = 5.508

Answer 2

At minimum cost, Length = 8 foot, Height = 18 foot

Explanation:

Volume of the closed rectangular shipping crate =
`1152ft^3`

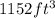
The crate has a square base from the given statement.

Therefore: Volume = Square Base Area X Height =
`l^2h`

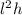
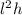`l^2h`=1152

`h=(1152)/(l^2)`

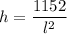
Total Surface Area of a Cuboid =2(lb+lh+bh)

Since we have a square base

Total Surface Area
`=2(l^2+lh+lh)`

The Total Surface Area of the Crate

= Area of Top + Area of Bottom + Area of Sides

`=l^2+l^2+4lh`

The material for the top and sides costs $2 per square foot and the material for the bottom costs $7 per square foot.

Therefore, Cost of the Material for the Crate

`C=7l^2+2(l^2+4lh)\\C=9l^2+8lh`

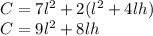
Recall earlier that we derived:
`h=(1152)/(l^2)`

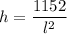
Substituting into the formula for the Total Cost

`C=9l^2+8l((1152)/(l^2))\\C=9l^2+(9216)/(l)\\C=(9l^3+9216)/(l)`

The minimum costs for the material occurs at the point where the derivative equals zero.

`C^(')=(18l^3-9216)/(l^2)=0\\18l^3-9216=0\\18l^3=9216\\l^3=512\\l=\sqrt[3]{512}=8`

Recall:

`h=(1152)/(l^2)=(1152)/(8^2)=18`

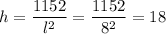
The dimensions that will minimize the cost of the box are: Length = 8 foot, Height = 18 foot