Question

A 75.0 kg ladder that is 3.00 m in length is placed against a wall at an angle theta. The center of gravity of the ladder is at a point 1.2 m from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.400. There is no friction between the wall and the ladder. What is the minimum angle the ladder makes with the horizontal for the ladder not to slip and fall

Answer 1

The minimum angle the ladder makes with the horizontal for the ladder not to slip and fall is 45 degrees.

Step-by-step explanation:

Given that,

Mass of the ladder, m = 75 kg

Length of the ladder, l = 3 m

The center of gravity of the ladder is at a point 1.2 m from the base of the ladder.

The coefficient of static friction at the base of the ladder is 0.4

We need to find the minimum angle the ladder makes with the horizontal for the ladder not to slip and fall.

At equilibrium, net force and net torque on the ladder is equal to zero. Force is given by :

`f=\mu mg`

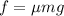
Using condition for torque as :

`mg* 12\cos\theta-fl\sin (180-\theta)=0\\\\mg* 1.2\cos\theta-\mu mgl\sin (180-\theta)=0\\\\\tan\theta=(1.2)/(\mu l)\\\\\tan\theta=(1.2)/(0.4* 3)\\\\\tan\theta=1\\\\\theta=45^(\circ)`

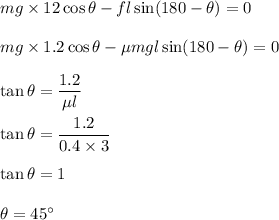
So, the minimum angle the ladder makes with the horizontal for the ladder not to slip and fall is 45 degrees.