Answer:
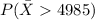
And the z score is given by:
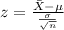
And using this formula we got:
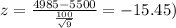
And using the complement rule and the normal tandard distribution or excel we got:

Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
Let X the random variable that represent the comprehensive strength of a population, and for this case we know the following info:
Where
 and
and
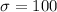
We select a sample size of n=9. Assuming that the distribution for X is normal then we can use the distribution for the sample mean
 is given by:
is given by:

And we want this probability:
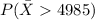
And the z score is given by:
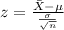
And using this formula we got:
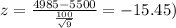
And using the complement rule and the normal tandard distribution or excel we got:
