Question

If a snowball melts so that its surface area decreases at a rate of 3 cm^2/min, find the rate at which the diameter decreases when the diameter is 11 cm.

Answer 1

The diameter is decreasing at the rate of 0.0434 cm/min.

Explanation:

A snowball is spherical, so it's area is given by the following formula:

`A = 4\pi r^(2)`

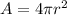
The radius is half the diameter, so:

`A = 4\pi ((d)/(2))^(2)`

`A = 4\pi ((d)/(2))^(2)`

`A = \pi d^(2)`

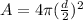
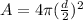
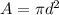
If a snowball melts so that its surface area decreases at a rate of 3 cm^2/min, find the rate at which the diameter decreases when the diameter is 11 cm.

This is
`(dd)/(dt)` when
`(dA)/(dt) = -3, d = 11`

`A = \pi d^(2)`

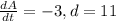
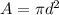
Applying implicit differentiation:

We have to variables(A and d), so:

`(dA)/(dt) = 2\pi d (dd)/(dt)`

`-3 = 22\pi (dd)/(dt)`

`(dd)/(dt) = -(3)/(22\pi)`

`(dd)/(dt) = -0.0434`

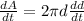
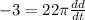
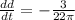
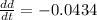
The diameter is decreasing at the rate of 0.0434 cm/min.