Question

A quality control inspector has drawn a sample of 16 light bulbs from a recent production lot. Suppose 20% of the bulbs in the lot are defective. What is the probability that between 5 and 7 (both inclusive) bulbs from the sample are defective? Round your answer to four decimal places.

Answer 1

Probability that between 5 and 7 (both inclusive) bulbs from the sample are defective is 0.1948.

Explanation:

We are given that quality control inspector has drawn a sample of 16 light bulbs from a recent production lot.

Suppose 20% of the bulbs in the lot are defective.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

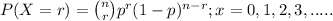
where, n = number of trials (samples) taken = 16 light bulbs

r = number of success = between 5 and 7 (both inclusive)

p = probability of success which in our question is % of bulbs in

the lot that are defective, i.e; 20%

LET X = Number of bulbs that are defective

So, it means X ~ Binom(
`n=16,p=0.20`)

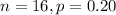Now, probability that between 5 and 7 (both inclusive) bulbs from the sample are defective is given by = P(5
`\leq` X
`\leq` 7)

P(5
`\leq` X
`\leq` 7) = P(X = 5) + P(X = 6) + P(X = 7)

=
`\binom{16}{5}* 0.20^(5) * (1-0.20)^(16-5)+ \binom{16}{6}* 0.20^(6) * (1-0.20)^(16-6)+ \binom{16}{7}* 0.20^(7) * (1-0.20)^(16-7)`

=
`4368 * 0.20^(5) * 0.80^(11) +8008 * 0.20^(6) * 0.80^(10) +11440 * 0.20^(7) * 0.80^(9)`

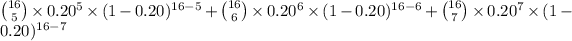
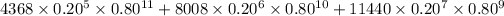
= 0.1948

Hence, the probability that between 5 and 7 (both inclusive) bulbs from the sample are defective is 0.1948.