Question

A community plans to build a facility to convert solar radiation to electrical power. The community requires 3.00 MW of power, and the system to be installed has an efficiency of 30.0% (that is, 30.0% of the solar energy incident on the surface is converted to useful energy that can power the community). Assuming sunlight has a constant intensity of 1 060 W/m2, what must be the effective area of a perfectly absorbing surface used in such an installation?

Answer 1

the effective area (A) of a perfectly absorbing surface used in such an installation must be = 9.433 × 10³ m²

Step-by-step explanation:

Given that:

intensity of sunlight = 1060 W/m²

We assume that A should represent the effective area of absorbing surface;

The required power P = 3.0 MW = 3.0 × 10⁶ W

Power of Sunlight on absorbing surface is as follows:

`P_(light) = IA \\\\P_(light) = 1060 \ * \ A`

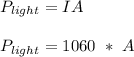
However ; from the given condition;

30% of
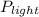`P_{light` = P

∴

`(30)/(100)*1060 *A = 3.0 *10^6\\ \\A = (3.0*10^6*100)/(30*1060)\\\\A = 9.433*10^3 \ m^2`

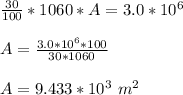
Therefore ; the effective area (A) of a perfectly absorbing surface used in such an installation must be = 9.433 × 10³ m²