Question

The orcs are cgarging toward Helm's Keep with ladders to climb up the famous 30-meter walls of the fortress. The orcs also know about the OSHA safety rule about having a 75 degree angle between the ladder & the ground.

part a.) how long should the ladder be to reach the top of the wall? round to the closest meter.


part b.) how far from the wall should the base of the ladder be for safe climbing?

Answer 1

a) 31.058 m

b) 8.04 m

Explanation:

Given that:

The angle between the ladder and the ground = 75°

Length of the wall = 30 m

Since the wall is perpendicular to the ground, the angle between the wall and the ground = 90°

a) Using sine rule which states that If a, b and c are the lengths of the sides opposite the angles A, B and C in a triangle,

`(a)/(sin(A)) =(b)/(sin(B)) =(c)/(sin(C))`

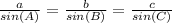
Let us assume the Length of the wall = a = 30 m

The opposite angle = A = The angle between the ladder and the ground = 75°

c = Length of the ladder to reach top of the wall

The opposite angle = C =the angle between the wall and the ground = 90°

Therefore:

`(a)/(sin(A)) =(c)/(sin(C)) \\c=(a*sin(C))/(sin(A)) \\c=(30*sin(90^0))/(sin(75^0)) =31.058m`

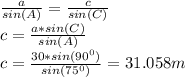
The length of the ladder is 31.058 m

b) Using Pythagoras theorem:

The length of the ladder = c, Length of the wall = a, Distance from wall to base of ladder = b

c² = a² + b²

31.058² = 30² + b²

964.6 = 900 + b²

b² = 964.6 - 900 = 64.6

b = √64.6 = 8.04

b = 8.04 m

The distance from the wall to the base of the ladder should be 8.04 m for safe climbing?