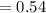Question

Find the probability of selecting none of the correct six integers in a lottery, where the order in which these integers are selected does not matter, from the positive integers not exceeding a) 40 b) 48 c) 56 d) 64.

Answer 1

Explanation:

Given

there are six integers to win a lottery

case-1 Integer not exceeding 40

no of ways to choose 6 incorrect numbers

`=(^(34)C_(6))/(^(40)C_(6))`

`=0.35`

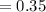
Case-2 no of ways to choose 6 incorrect numbers out of 48 integers

`=(^(42)C_(6))/(^(48)C_(6))`

`=0.427`

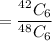
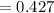
Case-3 no of ways to choose 6 incorrect numbers out of 56 integers

`(^(50)C_(6))/(^(56)C_(6))`

`=0.489`

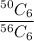
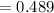
Cae-4 no of ways to choose 6 incorrect numbers out of 64 integers

`(^(58)C_(6))/(^(64)C_(6))`

`=0.54`