Question

Assuming you obtained a random sample of blood glucose levels from 32 individuals from a population and the mean of the population is 120 and the standard deviation of the sample is 15, calculate the probability that the mean blood glucose levels for the sample population will be above 127.

A. .9959
B. .5900
C. .4100
D. .0041

Answer 1

The option C) 0.0041 is correct

∴ the probability that the mean blood glucose levels for the sample population will be above 127 is 0.0041.

Explanation:

Given that Assuming you obtained a random sample of blood glucose levels from 32 individuals from a population and the mean of the population is 120 and the standard deviation of the sample is 15,

To calculate the probability that the mean blood glucose levels for the sample population will be above 127:

By using the Normal probability distribution and the Central limit theorem.

Normal probability distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a given data set with mean
`\mu` and standard deviation
`\sigma` , the z-score of a measure X is given by:

`Z=(x-\mu)/(\sigma)`

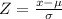
Total probability=p+q=1

Subtracting 1 by the p value, we get the probability that the value of the measure is greater than X.

Central Limit Theorem :

The Central Limit Theorem states that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma` , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean

For a skewed variable, the Central Limit Theorem for n is greater than 30.

Given that
`\mu=120` ,
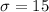`\sigma=15` , n=32

`s=(15)/(√(32))`

`s=(15)/(4(√(2)))`

`s=2.65`

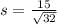
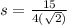
Now we have to Calculate the probability that the mean blood glucose levels for the sample population will be above 127.

This is 1 subtracted by the p value of Z when X = 127.

`Z=(x-\mu)/(\sigma)`

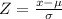
By the Central Limit Theorem

`Z=(x-\mu)/(s)`

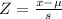
Substitute the values in the formula we get

`Z=(127-120)/(2.65)`

`=(7)/(2.65)`

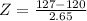
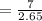
`Z=2.6415` has a p value of 0.9959

Now 1 subtracted by the p value of Z is 2.6415 when X = 127 is

1 - 0.9959 = 0.0041

∴ the probability that the mean blood glucose levels for the sample population will be above 127 is 0.0041.

∴ option C) 0.0041 is correct.