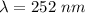Answer:
The wavelength of he radiation emitted is
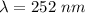
Step-by-step explanation:
We know that energy needed is given by
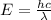
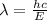 ----- (1)
----- (1)
h = 6.62 ×
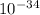 J s
J s
c = 3 ×
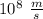
E = 786.4 - 310.8 = 475.6
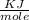
Total energy
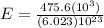
E = 78.9 ×
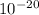 J
J
From equation (1)
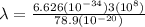
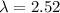 ×
×
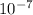
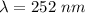
Therefore the wavelength of he radiation emitted is