Question

An article in the Washington Post on March 16, 1993 stated that nearly 45% of all Americans have brown eyes. A random sample of 55 students found 43 with brown eyes. Give the numerical value of the sample proportion, p^p^, and find the value of the test statistic. Sample Proportion p^=p^= (round to four decimal places). Test Statistic z=z= (round to four decimal places).

Answer 1

Sample proportion,
`\hat p` = 0.7818

Test statistics, z = 5.9577

Explanation:

We are given that an article in the Washington Post on March 16, 1993 stated that nearly 45% of all Americans have brown eyes. A random sample of 55 students found 43 with brown eyes.

Let p = population proportion Americans having brown eyes

SO, Null Hypothesis,
`H_0` : p = 45% {means that the proportion of all Americans having brown eyes is 45%}

Alternate Hypothesis,
`H_a` : p
`\\eq` 45% {means that the proportion of all Americans having brown eyes is different from 45%}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
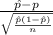`\frac{\hat p -p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of Americans having brown eyes in a sample of 55 students =
`(43)/(55)` = 0.7818

n = sample of students = 55

So, test statistics =
`\frac{0.7818-0.45}{\sqrt{(0.7818(1-0.7818))/(55) } }`

= 5.9577

Therefore, the value of test statistics, z = 5.9577.