Question

The mean weight of trucks traveling on a particular section of I-475 is not known. A state highway inspector needs an estimate of the mean. He selects a random sample of 49 trucks passing the weighing station and finds the sample mean is 15.8 tons. The population standard deviation is 3.8 tons. What is the 95 percent confidence interval for the population mean

Answer 1

The 95 percent confidence interval for the population mean is between 14.736 tons and 16.864 tons.

Explanation:

We have the population's standard deviation, so we can find the normal confidence interval.

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.95)/(2) = 0.025`

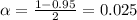
Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
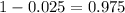`1-0.025 = 0.975`, so
`z = 1.96`

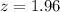
Now, find the margin of error M as such

`M = z*(\sigma)/(√(n))`

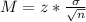
In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 1.96*(3.8)/(√(49)) = 1.064`

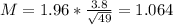
The lower end of the interval is the sample mean subtracted by M. So it is 15.8 - 1.064 = 14.736 tons

The upper end of the interval is the sample mean added to M. So it is 15.8 + 1.064 = 16.864 tons

The 95 percent confidence interval for the population mean is between 14.736 tons and 16.864 tons.