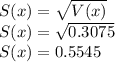Question

16. From past experience, a company has found that in cartons of transistors, 92% contain no defective transistors, 3% contain one defective transistor, 3% contain two defective transistors, and 2% contain three defective transistors. Find the mean, variance, and standard deviation for the defective transistors.

Answer 1

mean = 0.15

variance = 0.3075

standard deviation = 0.5707

Explanation:

- See the attachment an fill in the cells with "bold" marked columns.

- Where mean = E(X)

E(X) = Sum ( Xi*P(Xi) )

= 0 + 0.03 + 0.06 + 0.06

= 0.15

- The variance = Var (X)

Var (X) = Sum ( X2*P(X) ) - E(X)^2

= (0 + 0.03 + 0.12 + 0.18) - 0.15^2

= 0.3075

- The standard deviation = S(X)

S(X) = √Var(X) = √0.3075 = 0.5707

Answer 2

E(x)=0.15

V(x)=0.3075

S(x)=0.5545

Explanation:

The mean of a discrete variable is calculated as:

`E(x)=x_1*p(x_1)+x_2*p(x_2)+...+x_n*p(n)`

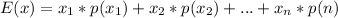
where
`x_1,x_2,...,x_n` are the values that the variable can take and
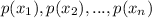`p(x_1),p(x_2),...,p(x_n)` are their respective probabilities.

So, if we call x the number of defective transistors in cartons, we can calculate the mean E(x) as:

`E(x)=(0*0.92)+(1*0.03)+(2*0.03)+(3*0.02)=0.15`

Because there are 0 defective transistor with a probability of 0.92, 1 defective transistor with a probability of 0.03, 2 defective transistors with a probability of 0.03 and 3 defective transistors with a probability of 0.01.

At the same way, the variance V(x) is calculated as:

`V(x)=E(x^2)-(E(x))^2`

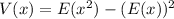
Where
`E(x^2)=x_1^2*p(x_1)+x_2^2*p(x_2)+...+x_n^2*p(n)`

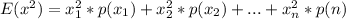
So, the variance V(x) is equal to:

`E(x^2)=(0^2*0.92)+(1^2*0.03)+(2^2*0.03)+(3^2*0.02)=0.33\\V(x)=0.33-(0.15)^2\\V(x)=0.3075`

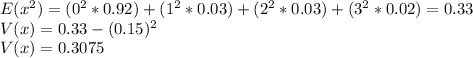
Finally, the standard deviation is calculated as:

`S(x)=√(V(x)) \\S(x)=√(0.3075) \\S(x)=0.5545`