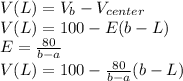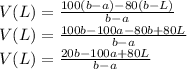Question

A long coaxial conducting cable is oriented along the z-axis. The Inner conductor is held at 20 volts and the outer conductor is held at 100 volts. the radius of the inner conductor is 'a' and the outer conductor 'b'. Find the Electric Potential, I and Electric Field, E between the cylinders.

Answer 1

a) The electric potential between the cylinders,
`V(L) = (20b - 100a + 80L)/(b-a)`

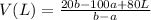
b) The electric field between the cylinders,
`E = (80)/(b-a)`

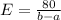
Step-by-step explanation:

Voltage at the inner conductor, V₁ = 20 volts

Voltage at the outer conductor, V₂ = 100 volts

Change in potential,
`\triangle V = V_(2) - V_(1)`

`\triangle V = 100 - 20\\\triangle V = 80 volts`

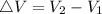
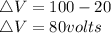
The change in potential is given by the formula:

`\triangle V = E(b-a)\\80 = E(b-a)`

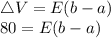
The electric field,
`E = (80)/(b-a)`

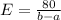
To get the electric potential at a certain point, L from the center:

The distance from the outer conductor to the center = b - L

The electric potential at L will be given by the equation:

`V(L) = V_(b) - V_(center) \\V(L) = 100 - E(b-L)\\E = (80)/(b-a) \\V(L) = 100 - (80)/(b-a)(b-L)`

`V(L) = (100(b-a) - 80(b-L))/(b-a) \\V(L) = (100b - 100a -80b + 80L)/(b-a) \\V(L) = (20b - 100a + 80L)/(b-a)`